№2(69), апрель – июнь 2015

Download full PDF version



Picture Details Pages Download
РЯБУХА Ю.Н. ТЕХНОЛОГИЯ БЫСТРОЙ ТРЕХМЕРНОЙ ОБРАБОТКИ ДИНАМИЧЕСКОГО ИНФОРМАЦИОННОГО РЕСУРСА В УСЛОВИЯХ МЕНЯЮЩЕГОСЯ СЕМАНТИЧЕСКОГО СОДЕРЖАНИЯ

УДК 621.327: 681.5

Показывается, что в сфере мониторинга объектов в кризисных ситуациях значительная роль принадлежит комплексам воздушного видеонаблюдения. Объясняется, что для систем аэромониторинга обеспечение информационной безопасности связано с выполнением требований по категориям доступности и целостности. Обосновывается возникновение проблемных вопросов относительно обеспечения безопасности динамических видеоинформационных потоков. Делается вывод относительно необходимости использования методов с дополнительным учетом межкадровой структурной избыточности в условиях меняющегося семантического содержания для кадров в видеопотоке. Излагаются основные этапы разработки технологии трехмерной обработки динамического видеоинформационного ресурса.

УДК 621.327: 681.5

Технологія швидкої тривимірної обробки динамічного інформаційного ресурсу в умовах змінного семантичного змісту / Ю.М. Рябуха //Радіоелектроніка та інформатика. 2015.  №2. С. 3-5.

Показано, що у сфері моніторингу об’єктів в кризових ситуаціях значна роль відводиться комплексам повітряного відеоспостереження. Обґрунтовано, що для систем аеромоніторингу забезпечення інформаційної безпеки пов’язане з виконанням вимог по категоріях доступності і цілісності.

Бібліогр.: 8 назв.

UDC 621.327: 681.5

Technology fast 3-d processing dynamic information resource in a changing semantic content / Yu. Ryabukha // Radioelektronika i informatika. 2015. N 2. P. 3-5.

Shown, that in the field monitoring of objects in crisis situations a considerable role gives oneself up complexes air video supervision. Grounded, that for the systems the air monitoring providing of informative safety is related to implementation requirements on the categories availability and integrity. rs on all of vertical lines.

Ref.: 8 items.

Литература:

  1. Лабутина И.А. Дешифрование аэрокосмических снимков: Учебное пособие. М: Аспект-Пресс, 2004. 184 с.
  2. Кашкин В.Б. Цифровая обработка аэрокосмических изображений: Конспект лекций. Красноярск : ИПК СФУ. 2008. 121 с.
  3. Горбулін В.П. Актуальні проблеми системного забезпечення інформаційної безпеки України / В.П. Горбулін, М.М. Биченок, П.М. Копка // Матер. міжнар. наук.-практ. конф. “Форми та методи забезпечення інформаційної безпеки держави”. К.: Національна академія СБ України. 2008. С. 79 – 85.
  4. Баранник В.В. Структурно-комбинаторное представление данных в АСУ / В.В. Баранник, Ю.В. Стасев, Н.А. Королева. Х.: ХУПС, 2009. 252 с.
  5. Баранник В.В. Метод компрессии видеопотока на основе полиадического кодирования предсказываемых кадров / В.В. Баранник, Ю.Н. Рябуха, Н.А. Харченко // Радиоэлектроника и информатика. № 2. 2013.  С. 23 ‑ 28.
  6. Рябуха Ю.Н. Метод кодирования трехмерных структур данных по вертикально-горизонтальной архитектуре // Сучасна спеціальна техніка. К.: ДНДІ МВС України. 2014. № 1. С. 12 ‑ 21.
  7. Рябуха Ю.Н. Метод трехмерного дифференциального межкадрового кодирования без потери целостности информационного ресурса // АСУ и приборы автоматики. 2014. № 169. С. 22 ‑ 30.
  8. Рябуха Ю.Н. Технология трехуровневой параллельной реализации трехмерного кодирования структур видеоданных // АСУ и приборы автоматики. 2013. № 165. С 3 ‑ 7.

Transliterated bibliography:

  1. Labutina I.A. Deshifrovanie ajerokosmicheskih snimkov: Uchebnoe posobie. M: Aspekt-Press, 2004. 184 s.
  2. Kashkin V.B. Cifrovaja obrabotka ajerokosmicheskih izobrazhenij: Konspekt lekcij. Krasnojarsk : IPK SFU. 2008. 121 s.
  3. Gorbulіn V.P. Aktual'nі problemi sistemnogo zabezpechennja іnformacіjnoї bezpeki Ukraїni / V.P. Gorbulіn, M.M. Bichenok, P.M. Kopka // Mater. mіzhnar. nauk.-prakt. konf. “Formi ta metodi zabezpechennja іnformacіjnoї bezpeki derzhavi”. K.: Nacіonal'na akademіja SB Ukraїni. 2008. S. 79 – 85.
  4. Barannik V.V. Strukturno-kombinatornoe predstavlenie dannyh v ASU / V.V. Barannik, Ju.V. Stasev, N.A. Koroleva. H.: HUPS, 2009. 252 s.
  5. Barannik V.V. Metod kompressii videopotoka na osnove poliadicheskogo kodirovanija predskazyvaemyh kadrov / V.V. Barannik, Ju.N. Rjabuha, N.A. Harchenko // Radiojelektronika i informatika. № 2. 2013. S. 23   28.
  6. Rjabuha Ju.N. Metod kodirovanija trehmernyh struktur dannyh po vertikal'no-gorizontal'noj arhitekture // Suchasna specіal'na tehnіka. K.: DNDІ MVS Ukraїni. 2014. № 1. S. 12-21.
  7. Rjabuha Ju.N. Metod trehmernogo differencial'nogo mezhkadrovogo kodirovanija bez poteri celostnosti informacionnogo resursa // ASU i pribory avtomatiki. 2014. № 169. S. 22-30.
  8. Rjabuha Ju.N. Tehnologija trehurovnevoj parallel'noj realizacii trehmernogo kodirovanija struktur videodannyh // ASU i pribory avtomatiki. 2013. № 165. S. 3-7.

Рябуха Юрий Николаевич, канд. техн. наук, соискатель Харьковского университета Воздушных Сил. Научные интересы: информационно-телекоммуникационные технологии, кодирование, защита и передача информации. Адрес: Украина, 61023, Харьков, ул. Сумская 77/79, тел. 8 050-3038971.

 3-5
ПАНКРАТОВ А.В. PHI-ФУНКЦИИ ДЛЯ ЭЛЛИПСОВ, АППРОКСИМИРОВАННЫХ ДУГАМИ ОКРУЖНОСТЕЙ

УДК 519.85

Рассматривается задача оптимальной упаковки аппроксимированных дунами окружностей эллипсов, допускающих непрерывные вращения. Для аналитического описания основных ограничений размещения предлагаются свободные от радикалов phi-функции, имеющие существенно более простую форму записи и меньшую вычислительную сложность, чем известные аналоги.

Ключевые слова: раскрой и упаковка, эллипсы, аппроксимация, phi-функция.

Key words: cutting and packing, ellipses, approximation,   phi-function.

УДК 519.85

Phi-функції для еліпсів, апроксимованих дугами кіл / О.В. Панкратов // Радiоeлектронiка та iнформатика. 2015. № 2. С. 6–9.

Розглянута задача упаковки набору нерівних по величині еліпсів, що можуть вільно транслюватися і обертатися, у прямокутний контейнер мінімального розміру. Для розробки ефективних алгоритмів оптимізації, заснованих на використанні методів локальної та глобальної оптимізації, побудовані адекватні математичні моделі на ґрунті аналітичного опису відносин еліпсів. Для опису обмежень неперетину і належності виведено нові вільні від радикалів phi-функції для еліпсів, що апроксимовані дугами кола.

Іл. 4. Бібліогр.: 13 назв.

UDC 519.85

Phi-functions for ellipses approximated by circular arcs / A.V. Pankratov // Radioelektronika i informatika. 2015. N 2. P. 6-9.

The problem of packing a set of nonequal ellipses, allowing continuous rotation and translation in a minimum size rectangular container is considered. To develop efficient optimization algorithms based on the use of methods of local and global optimization, adequate mathematical models based on analytical description of the relationship of the ellipses to be built. For  describing  nonoverlapping  and  containment  constraints,  new radical-free phi-functions  are derived  for  ellipses  approximated  by  circle  arcs.

Fig. 4. Ref.: 13 items.

Литература:

  1. Wаscher G., Hauner H. and Schumann H. An improved typology of cutting and packing problems // European Journal of Operational Research. 2007. Volume 183, Issue 3, 16. P. 1109-1130.
  2. Bennell J.A. and Oliveira J. F. The geometry of nesting problems: A tutorial // European J. Operational Research. 2008. 184. P. 397-415.
  3. Chazelle B., Edelsbrunner H., Guibas L.J. The complexity of cutting complexes // Discrete & Computational Geometry. 1989. 4(2), P. 139-181.
  4. Birgin E.G., Bustamante L.H., Callisaya H.F., Martэnez, J.M. Packing circles within ellipses // International transactions in operational research. 2013. № 20. P. 365–389.
  5. Xu W.X., Chen H.S., Lv Z. An overlapping detection algorithm for random sequential packing of elliptical particles// Physica. 2011. A. 390. P. 245-267.
  6. Kallrath J. and Rebennack S. Cutting Ellipses from Area-Minimizing Rectangles. // Journal of Global Optimization. 2013. DOI10.1007/s10898-013-0125-3.
  7. Kallrath, J. Cutting Circles and Polygons from Area-Minimizing Rectangles. // Journal of Global Optimization. 2009. 43. P. 299–328.
  8. Stojan Ju.G., Pankratov A.V., Romanova T.E., Chernov N.I. Kvazi-phi-funkcii dlja matematicheskogo modelirovanija otnoshenij geometricheskih ob#ektov // Dopovіdі Nacіonal’noї akademії nauk Ukraїni. 2014. № 9.  Р. 49-54.
  9. Pankratov A., Romanova T. Subbota I. Optimal’naja upakovka jellipsov s uchetom dopustimyh rasstojanij. // Zhurnal obisljuval’noї ta prikladnoї matmatiki. 2014. 1. Р. 129-140.
  10. Chernov N, Stoyan Y, Romanova T. Mathematical model and efficient algorithms for object packing problem // Computational Geometry: Theory and Applications. 2010. 43(5). P. 535-553.
  11. Bennell J., Scheithauer G., Stoyan Yu., Romanova T., Pankratov A. Optimal clustering of a pair of irregular objects // Journal of Global Optimisation, March 2015, Volume 61, Issue 3. P. 497-524.
  12. Chernov N. , Stoyan Y., Romanova T., Pankratov A.  Phi-Functions for 2D Objects Formed by Line Segments and Circular Arcs // Advances in Operations Research. 2012. vol. Article ID 346358. 26 pages. ­doi:10.1155/2012/346358.
  13. Pankratov A.V., Romanova T.E., Subbota I.A. Razrabotka jeffektivnyh algoritmov optimal’noj upakovki jellipsov // Vostochno-Evropejskij zhurnal peredovyh tehnologij. 2014. 5/4(71). Р. 28-35.

Панкратов Александр Викторович, д-р техн. наук, старший научный сотрудник отдела математического моделирования и оптимального проектирования  института проблем машиностроения им. А.Н. Подгорного НАН Украины. Научные интересы: задачи раскроя и упаковки, нелинейная оптимизация, исследование операций. Адрес: Украина, 61046,  Харьков, ул. Дм. Пожарского, 2/10, тел. (057)3494777.

Pankratov Alexander Victorovich, Dr. of Science, tech. senior research scientist of the A.N. Podgorny Institute for Mechanical Engineering Problems of the National   Academy of Sciences of Ukraine. Sientific subjects: cutting and packing problems, nonlinear optimization, operational research. Ukraine, 61046, Kharkov, ul. Dm. Pozharsky, 2/10, tel. (057) 3494777.

 6-9
ГИБКИНА Н.В., МАРТЫНЕНКО М.С., СИДОРОВ М.В. ОБ ОДНОЙ ЗАДАЧЕ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ НАГРЕВОМ ОДНОРОДНОЙ ПЛАСТИНЫ

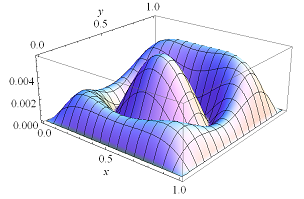
Рассматривается одна из возможных постановок задач оптимального управления нагревом однородной пластины. Под оптимальным управлением понимается такой режим нагрева сторон пластины, при котором в конечный момент времени в пластине устанавливается температурный режим, наиболее близкий (в смысле среднеквадратической метрики) к желаемому распределению температур.

УДК 517.977.56

Про одну задачу оптимального керування нагріванням однорідної пластини / Н.В. Гибкіна, М.С. Мартиненко, М.В. Сидоров // Радіоелектроніка та інформатика. 2015. № 2. С. 10 – 16.

Розглянуто одну з можливих постановок задач оптимального керування нагріванням однорідної пластини. Визначено такий температурний режим нижньої сторони пластини, що у кінцевий момент часу приводить до розподілу температури у всій пластині, якомога близького до бажаного розподілу. Наведено результати розв’язання задачі оптимального керування для різних типів бажаного розподілу температури та для апроксимуючих співвідношень функції керування у вигляді відрізків подвійного ряду Фур’є різної довжини.

Іл. 8. Бібліогр.: 14 назв.

UDC 517.977.56

About one problem of optimal control of the heating of a homogeneous plate / N.V. Gybkina, M.S. Martynenko, M.V. Sidorov // Radioelektronika i informatika. 2015. № 2 P. 10–16.

The one of the possible formulations of optimal control problems by heating a homogeneous plate was considered. Such temperature mode of the lower side of the plate, which leads to the temperature distribution in the plate at the final moment of time as close as possible to the specified distribution was defined. The results of solving the optimal control problem for different types of specified temperature distribution and for approximating expression of control functions in the form of segments of double Fourier series of different lengths were obtained.

Fig. 8. Ref.: 14 items.

Литература:

  1. Бутковский А.Г. Теория оптимального управления системами с распределенными параметрами. М.: Наука, 1965. 474 c.
  2. Бутырин В.И., Фильштинский Л.А. Оптимальное управление температурным полем в стержне при программном изменении зоны управления // Прикладная механика. 1976. Т. 12, №8. С. 115 – 118.
  3. Вабищевич П.Н. Вычислительные методы математической физики. Обратные задачи и задачи управления. М.: Вузовская книга, 2009. 268 с.
  4. Васильев Ф.П. Методы оптимизации: В 2-х кн. Ч. II. Мн.: МНЦНМО, 2011. 434 с.
  5. Лионс Ж.-Л. Оптимальное управление системами, описываемыми уравнениями с частными производными. М.: Мир, 1972. 416 с.
  6. Лисковец О.А. Вариационные методы решения неустойчивых задач. М.: Наука и техника, 1981. 344 с.
  7. Мартинсон Л.К., Малов Ю.И. Дифференциальные уравнения математической физики. 2-е изд. М.: Изд-во МГТУ им. Н.Э. Баумана, 2002. 368 с.
  8. Самарский А.А., Вабищевич П.Н. Вычислительная теплопередача. М.: Едиториал УРСС, 2003. 784 с.
  9. Свешников А.Г., Боголюбов А.Н., Кравцов В.В. Лекции по математической физике. М.: Наука, 2004. 416 с.
  10. Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Наука, 2004. 798 с.
  11. Фурсиков А.В. Оптимальное управление распределенными системами. Теория и приложения. Новосибирск: Научная книга, 1999. 352 с.
  12. Гибкина Н.В., Подусов Д.Ю., Сидоров М.В. Оптимальное управление конечным температурным состоянием однородного стержня // Радиоэлектроника и информатика. 2014. №2. С. 9-15.
  13. Клопотов В.Д., Нестеренко В.П. Математическое моделирование тепловых процессов в режущем инструменте // Изв. Томского политехнического университета. 2005. Т. 308, № 3. С.125-128.
  14. Коновалов В.И., Пахомов А.Н., Гатапова Н.Ц., Колиух А.Н. Методы решения задач тепломассопереноса. Теплопроводность и диффузия в неподвижной среде: учеб. пособие. Тамбов: Изд-во ТГТУ, 2005. 80 с.

Transliterated bibliography:

  1. Butkovskij A.G. Teorija optimal'nogo upravlenija sistemami s raspredelennymi parametrami. M.: Nauka, 1965. 474 p.
  2. Butyrin V.I., Fil'shtinskij L.A. Optimal'noe upravlenie temperaturnym polem v sterzhne pri programmnom izmenenii zony upravlenija // Prikladnaja mehanika. 1976. T. 12, №8. P. 115 – 118.
  3. Vabishhevich P.N. Vychislitel'nye metody matematicheskoj fiziki. Obratnye zadachi i zadachi upravlenija. : Vuzovskaja kniga, 2009. 268 p.
  4. Vasil'ev F.P. Metody optimizacii: V 2-h kn. Ch. II. Mn.: MNCNMO, 2011. 434 p.
  5. Lions Zh.-L. Optimal'noe upravlenie sistemami, opisyvaemymi uravnenijami s chastnymi proizvodnymi. M.: Mir, 1972. 416 p.
  6. Liskovec O.A. Variacionnye metody reshenija neustojchivyh zadach. M.: Nauka i tehnika, 1981. 344 p.
  7. Martinson L.K., Malov Ju.I. Differencial'nye uravnenija matematicheskoj fiziki. 2-e izd. M.: Izd-vo MGTU im. N.Je. Baumana, 2002. 368 p.
  8. Samarskij A.A., Vabishhevich P.N. Vychislitel'naja teploperedacha. M.: Editorial URSS, 2003. 784 p.
  9. Sveshnikov A.G., Bogoljubov A.N.. Kravcov V.V. Lekcii po matematicheskoj fizike. M.: Nauka, 2004. 416 p.
  10. Tihonov A.N., Samarskij A.A. Uravnenija matematicheskoj fiziki. M.: Nauka, 2004. 798 p.
  11. Fursikov A.V. Optimal'noe upravlenie raspredelennymi sistemami. Teorija i prilozhenija. Novosibirsk: Nauchnaja kniga, 1999. 352 p.
  12. Gybkina N.V., Podusov D.Ju., Sidorov M.V. Optimal'noe upravlenie konechnym temperaturnym sostojaniem odnorodnogo sterzhnja // Radiojelektronika i informatika, №2. – 2014. – P. 9-15.
  13. Klopotov V.D., Nesterenko V.P. Matematicheskoe modelirovanie teplovyh processov v rezhushhem instrumente // Izvestija Tomskogo politehnicheskogo universiteta, № 3, T. 308. – 2005. – P.125-128.
  14. Konovalov V.I., Pahomov A.N., Gatapova N.C., Koliuh A.N. Metody reshenija zadach teplomassoperenosa. Teploprovodnost' i diffuzija v nepodvizhnoj srede: ucheb. posobie. Tambov: Izd-vo TGTU, 2005. 80 p.

Гибкина Надежда Валентиновна, канд. техн. наук, доц. каф. прикладной математики ХНУРЭ. Научные интересы: математическое моделирование, оптимальное управление и его приложения, математическая физика, актуарная и финансовая математика. Адрес: Украина, 61166, Харьков, пр. Ленина, 14, тел. (057) 7021436.

Мартыненко Михаил Сергеевич, студент группы СА-11-1 факультета прикладной математики и менеджмента ХНУРЭ. Научные интересы: математическое моделирование и оптимальное управление, программирование. Адрес: Украина, 61166, Харьков, пр. Ленина, 14, тел. (057) 7021436.

Сидоров Максим Викторович, канд. физ.-мат. наук, доц. каф. прикладной математики ХНУРЭ. Научные интересы: математическое моделирование, численные методы, математическая физика, теория R-функций и её приложения, стохастический анализ и его приложения. Адрес: Украина, 61166, Харьков, пр. Ленина, 14, тел. (057) 7021436.

Gybkina (Gibkina) Nadezhda Valentinovna, Ph.D. in Engineering, associate professor, associate professor of Department of Applied Mathematics KhNURE. Research interests: mathematical modeling, optimal control and its applications, mathematical physics, actuarial and financial mathematics. Address: Ukraine, 61166, Kharkov, Lenin Ave, 14, phone +38 (057) 7021436.

Martynenko Mikhail Sergeevich, student of Department of Applied Mathematics KhNURE. Research interests: mathematical modeling and optimal control, programming. Address: Ukraine, 61166, Kharkov, Lenin Ave, 14, phone +38 (057) 7021436.

Sidorov Maxim Victorovich, Ph.D. in Physics and Maths, associate professor, associate professor of Department of Applied Mathematics KhNURE. Research interests: mathematical modeling, numerical methods, mathematical physics, R-functions theory and its applications, stochastic analysis and its applications. Address: Ukraine, 61166, Kharkov, Lenin Ave, 14, phone +38 (057) 7021436.

 10-16
ЛУХАНІН В.С. ПРО ПОБУДОВУ ДВОСТОРОННІХ НАБЛИЖЕНЬ ДО ДОДАТНОГО РОЗВ’ЯЗКУ ЕЛІПТИЧНОЇ КРАЙОВОЇ ЗАДАЧІ З ЕКСПОНЕНЦІАЛЬНОЮ МАЖОРАНТОЮ

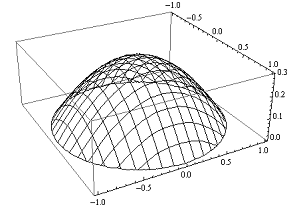
Розглядаються питання існування, єдиності та побудови двосторонніх наближень до додатного розв’язку однієї еліптичної крайової задачі з експоненціальною нелінійністю. Описуються умови, яким мають задовольняти параметри, що входять до нелінійності, щоб двосторонні наближення можна було побудувати.

Ключові слова: двосторонні наближення, інваріантний конусний відрізок, додатний розв’язок.

Key words: two-sided approximations, invariant cone segment, positive solution.

УДК 519.713

Про побудову двосторонніх наближень до додатного розв’язку еліптичної крайової задачі з експоненціальною мажорантою / В.С. Луханін // Радiоeлектронiка та iнформатика. 2015. № 2. С.16-18.

Розглянуто питання існування, єдиності та побудови двосторонніх наближень до додатного розв’язку однієї еліптичної крайової задачі з експоненціальною нелінійністю. Отримано умови, яким мають задовольняти параметри, що входять до нелінійності, щоб двосторонні наближення збіглися до додатного розв’язку розглядуваної задачі. Обчислювальний експеримент проведено у крузі, результати представлено у вигляді графіків поверхні наближення та ліній рівня, а також у вигляді таблиці.

Табл. 1. Іл. 2. Бібліогр.: 3 назви.

UDC 519.713

On the construction of two-sided approximations to the positive solution of the elliptic boundary value problem with exponential dominant / V.S. Lukhanin // Radioelektronika i informatika. 2015. N 2. P.16-18.

In this paper the existence, uniqueness and possibility of constructing of two-sided approximations to the positive solution of the elliptic boundary problem with exponential nonlinearity are considered.Conditions that parameters, which are included into the nonlinear part, must satisfy are obtained. The conditions guarantee that two-sided approximations converge to the positive solution of the problem. The computational experiment is performed in disk, the results of the experiment are presented as plots of approximate solution surface and level lines and also as a table.

Tab. 1. Fig. 2. Ref.: 3 items.

Література:

  1. S. Baraket, Ye. Dong. Singular Limit Solutions for Two-Dimensional Elliptic Problems with Exponentially Dominated Nonlinearity // Chinese Annals of Mathematics. Series B. 2001. V. 22, № 3 P. 287–296.
  2. Красносельский М.А. Положительные решения операторных уравнений. М.: Физматгиз, 1962. 394 с.
  3. Опойцев В.И. Обобщение теории монотонных и вогнутых операторов // Труды Моск. матем. общества. 1978. Т. 36. С. 237–273.

Transliterated bibliography:

  1. S. Baraket, Dong Ye. Singular Limit Solutions for Two-Dimensional Elliptic Problems with Exponentially Dominated Nonlinearity // Chinese Annals of Mathematics. Series B. 2001. V. 22, № 03 P. 287–296.
  2. Krasnosel'skij M.A. Polozhitel'nye resheniya operatornyx uravnenij. M.: Fizmatgiz, 1962. 394 s.
  3. Opojcev V.I. Obobshhenie teorii monotonnyx i vognutyx operatorov // Trudy Mosk. matem. obshhestva. 1978. T. 36. S. 237–273.

Луханін Володимир Сергійович, магістр, аспірант кафедри ПМ ХНУРЕ, інженер-програміст в EPAM Systems. Наукові інтереси: розв’язання крайових задач для диференціальних рівнянь у частинних похідних. Хоббі: читання, спорт. Адреса: Україна, 61103, Харків, вул. Космонавтів, 5А, кв. 2, тел. +38(063) 643-40-47.

Volodymyr Lukhanin, master, postgraduate student at the Department of Applied Mathematics of Kharkiv National University of Radio and Electronics, software engineer at EPAM Systems. Scientific interests: solving boundary value problems for partial differential equations. Hobby: reading, sports. Address: 61103, Ukraine, Kharkiv, Kosmonavtiv str. 5А, apt. 2, phone +38(063) 643-40-47.

 16-18
ШКИЛЬ А.С. ПОИСК ОШИБОК ПРОЕКТИРОВАНИЯ В ПОВЕДЕНЧЕСКИХ HDL-МОДЕЛЯХ МЕТОДОМ ОБРАТНОГО ПРОСЛЕЖИВАНИЯ

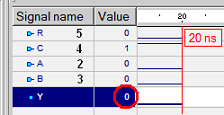
Предлагается метод поиска ошибок проектирования в HDL-моделях цифровых устройств поведенческого стиля описания. В качестве ошибок проектирования рассматривается замена операндов в арифметических или логических выражениях. Для повышения глубины поиска ошибок проектирования применяется метод обратного прослеживания в эквивалентных схемах функционально-блочного уровня с использованием кубического исчисления. Приводится пример реализации метода для фрагмента VHDL-модели арифметико-логического устройства.

УДК 681.326

Пошук помилок проектування у поведінкових HDL-моделях методом зворотного простежування / О.С. Шкіль  // Радіоелектроніка та інформатика. 2015. № 2. С. 19 – 25.

Запропоновано метод пошуку помилок проектування в HDL-моделях цифрових пристроїв поведінкового стилю опису. Як помилка проектування розглянута заміна операндів в арифметичних або логічних виразах. Для підвищення глибини пошуку помилок проектування застосовано метод зворотного простежування в еквівалентних схемах функціонально-блочного рівня з використанням кубічного числення. Наданий приклад реалізації метода для фрагменту VHDL-моделі арифметично-логічного пристрою.

Табл. 4. Іл. 9. Бібліогр.: 3 назви.

УДК 681.326

Design errors searching in behavioral HDL-models using the method of backtracking / A.S. Shkil  // Radioelektronika i informatika. 2015. № 2 P. 19–25.

In this paper the method of design errors searching in behavioral HDL-models of digital devices was proposed. Replacement of the operands in the arithmetic or logical expressions is considered as design errors. To increase the depth of design errors searching the method of backtracking in the equivalent circuit of the functional-block level using the cubic calculus was applied. An example of the method implementation for the fragment of the VHDL-model of the arithmetic logic unit was demonstrated.

Tab. 4. Fig. 9. Ref.: 3 items.

Литература:

1.Шкиль А.С. Структурное и функциональное диагностирование HDL-моделей цифровых устройств в САПР РЭА /А.С. Шкиль, Е.Е. Сыревич, С. Альмадхоун, Г.П. Фастовец // Інформаційно-керуючі системи на залізничному транспорті. 2013. № 2. C. 75-82.

2.Шкиль А.С. Поиск ошибок проектирования в HDL-моделях цифровых устройств / А.С. Шкиль, Е.Е. Сыревич, С. Альмадхоун // Інформаційні технології та комп’ютерна інженерія: міжнародна науково-практична конф., Вінниця, 19-21травня 2010. Вінниця, ВНТУ, 2010. C. 377-378.

3.Шкиль А.С. Метод обратного прослеживания для поиска ошибок проектирования в HDL-коде / А.С. Шкиль, Е.Е. Сыревич, Д.Е. Кучеренко, С. Альмадхоун // Радиоэлектроника. Информатика. Управление. 2009. №2. C. 86-90.

Transliterated bibliography:

1.Shkil' A.S. Strukturnoe i funkcional'noe diagnostirovanie HDL-modelej cifrovyh ustrojstv v SAPR RJeA /A.S. Shkil', E.E. Syrevich, S. Al'madhoun, G.P. Fastovec // Іnformacіjno-kerujuchі sistemi na zalіznichnomu transportі. 2013. № 2. C. 75-82.

2.Shkil' A.S. Poisk oshibok proektirovanija v HDL-modeljah cifrovyh ustrojstv / A.S. Shkil', E.E. Syrevich, S. Al'madhoun // Іnformacіjnі tehnologії ta komp’juterna іnzhenerіja: mіzhnarodna naukovo-praktichna konf., Vіnnicja, 19-21travnja 2010. Vіnnicja, VNTU, 2010. C. 377-378.

3.Shkil' A.S. Metod obratnogo proslezhivanija dlja poiska oshibok proektirovanija v HDL-kode / A.S. Shkil', E.E. Syrevich, D.E. Kucherenko, S. Al'madhoun // Radiojelektronika. Informatika. Upravlenie. 2009. №2. C. 86-90.

Шкиль Александр Сергеевич, канд. техн. наук, доцент кафедры АПВТ ХНУРЭ. Научные интересы: логическое моделирование, техническая диагностика компьютерных систем. Адрес: Украина, 61166, Харьков, пр. Ленина, 14, комн. 319.
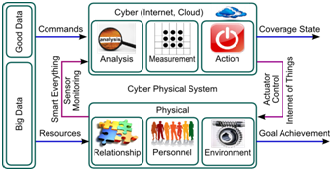ХАХАНОВ В.И., ЛИТВИНОВА Е.И., ЗАЙЧЕНКО С.А., ГУРЕЕВ Б.Н., ШЛЯХТУН М.М. КИБЕРФИЗИЧЕСКИЕ СТРУКТУРЫ ДЛЯ АНАЛИЗА БОЛЬШИХ ДАННЫХ

Предлагается инфраструктура обеспечения параллельного анализа big data для поиска, распознавания и принятия решений на основе использования булеановой метрики измерения киберпространства. Она характеризуется наличием единственной логической xor-операции для определения кибер-расстояния путем циклического замыкания не менее одного объекта, что дает возможность на порядок повысить быстродействие анализа больших данных. Разрабатывается новая структурная модель анализа big data, которая характеризуется использованием облачных сервисов, киберфизических и поисковых систем, параллельных виртуальных мультипроцессоров с минимальным набором векторно-логических операций для точного поиска информации на основе предложенной булеановой метрики и нечисленных критериев качества. Это дает возможность создавать семантическую инфраструктуру «чистого» киберпространства путем компетентностной классификации и метрического упорядочения big data в масштабах киберэкосистемы планеты.

УДК 004:519.713

Кіберфізичні структури для аналізуа великих даних  / В.І. Хаханов, Є.І. Литвинова,  С.О. Зайченко, Б.М. Гурєєв, М.М. Шляхтун // Радіоелектроніка та інформатика. 2015. № 2. С. 25–29.

Показана нова модель аналізу big dat, яка використовує кошти хмарних сервісів, кіберфізичні системи, паралельні віртуальні мультипроцесори з мінімальним набором векторно-логічних операцій для точного пошуку інформації на основі запропонованої булеанової метрики і векторно-логічних критеріїв якості, що дає можливість поступової класифікації та впорядкування даних на основі компетентнісної інфраструктурізаціі big data в масштабах кіберекосистеми планети.

Іл. 3. Бібліогр.: 7 назв.

UDC 004:519.713

Metrics and Structures for Big Data Analysis / V. I. Hahanov, E. I. Litvinova, S.A. Zaychenko, B.M. Gureev, M.M. Shlyahtun // Radioelektronika i informatika. 2015. № 2 P. 25–29.

A new model for analyzing big data, based on the use of cloud services, cyber physical systems, parallel virtual multiprocessors with a minimal set of vector-logical operations for accurate information retrieval by using the proposed Boolean metric and vector-logical quality criteria is shown; it allows gradual classifying and ordering data based on the competency structuring big data in the frame of the planet cyber-ecosystem.

Fig. 3. Ref.: 7  items.

Литература:

  1. Hasan Alkhatib, Paolo Faraboschi, Eitan Frachtenberg, Hironori Kasahara, Danny Lange, Phil Laplante, Arif Merchant, Dejan Milojicic, Karsten Schwan. IEEE CS 2022 Report. IEEE Computer Society. 2014. 163 p.
  2. [http://www.tssonline.ru/articles2/fix-corp/rost-obema-informatsii—realii-tsifrovoy-vselennoy# sthash.rpNOdQLF.dpuf]
  3. Бондаренко М.Ф., Хаханов В.И., Литвинова Е.И. Структура логического ассоциативного мультипроцессора // Автоматика и телемеханика. 2012. № 10. С. 71-92.
  4. Vladimir Hahanov, Wajeb Gharibi, Kudin A.P., Ivan Hahanov, Ngene Cristopher (Nigeria), Tiekura Yeve (Cоte d’Ivoire), Daria Krulevska, Anastasya Yerchenko, Alexander Mishchenko, Dmitry Shcherbin, Aleksey Priymak. Cyber Physical Social Systems – Future of Ukraine // Proceedings of 12th IEEE EWDT Symposium, Kiev, Ukraine, September 26-29. 2014. P. 67-81.
  5. Han Hu, Yonggang Wen, Tat-Seng Chua, Xuelong LiP. Toward Scalable Systems for Big Data Analytics: A Technology Tutorial. IEEE Explore: 2014. ISSN: 2169-3536. P. 652 – 687.
  6. Fadi H. Gebara, H. Peter Hofstee, and Kevin J. Nowka, IBM Research–Austin. Second-Generation Big Data Systems. IEEE Computer magazine. 2015, January. P. 36-41. 7. PureData System for Analytics: http://www-01.ibm.com/common/ssi/cgi-bin/ssialias?subtype=SP&infotype=PM&appname=SWGE_WA_ UZ_USEN&htmlfid=WAS12385USEN&attachment= WAS12385USEN.PDF#loaded

Хаханов Владимир Иванович, декан факультета КИУ ХНУРЭ, д-р техн. наук, профессор кафедры АПВТ ХНУРЭ, IEEE Senior Member, IEEE Computer Society Golden Core Member. Научные интересы: техническая диагностика цифровых систем, сетей и программных продуктов. Увлечения: баскетбол, футбол, горные лыжи. Адрес: Украина, 61166, Харьков, пр. Ленина, 14, тел. +380 57 70-21-326. E-mail: hahanov@kture.kharkov.ua.

Литвинова Евгения Ивановна, д-р техн. наук, профессор кафедры АПВТ ХНУРЭ, зам. декана факультета КИУ ХНУРЭ, IEEE Member. Научные интересы: техническая диагностика цифровых систем, сетей и программных продуктов. Увлечения: музыка. Адрес: Украина, 61166, Харьков, пр. Ленина, 14, тел. +3805770-21-326. E-mail: kiu@kture.kharkov.ua.

Зайченко Сергей Александрович, канд. техн. наук, доцент кафедры АПВТ ХНУРЭ. Научные интересы: автоматизированное проектирование и верификация цифровых систем. Увлечения: технологии онлайн-образования. Адрес: Украина, 61045, Харьков, ул. Космическая, 23а, тел. (057)-760-47-25.

Гуреев Богдан Николаевич, магистрант факультета КИУ ХНУРЭ, инженер-программист ООО “Алдек-КТС” (Харьков). Научные интересы: автоматизированное проектирование и верификация цифровых систем. Адрес: Украина, 61045, Харьков, ул. Космическая 23а, тел. (057)-760-47-25.

Шляхтун Максим Михайлович, магистрант факультета КИУ ХНУРЭ, инженер-программист ООО “Алдек-КТС” (г. Харьков). Научные интересы: автоматизированное проектирование и верификация цифровых систем. Адрес: Украина, 61045, Харьков, ул. Космическая 23а, тел. (057)-760-47-25.

 25-29
БОЖИНСКИЙ И.А. МЕТОДЫ И ТЕХНОЛОГИИ ИНТЕГРАЦИИ ИНФОРМАЦИОННЫХ СИСТЕМ И РАСПРЕДЕЛЕННЫХ БАЗ ДАННЫХ

Интеграция информационных ресурсов на уровне единого информационного пространства (ЕИП) - стратегическое направление в области управления информацией. Показывается, что современное состояние интеграционных технологий, моделей и методов решения поставленной проблемы в настоящее время не позволяет эффективно решать множество практических задач из-за функциональной ограниченности существующих подходов.

Ключевые слова: информационная система, интеграция данных, модель данных, предметная область, формальные системы.

УДК 621.383.52:537.311.4

Розробка технології і апаратури управління  коригуванням легуючих домішок для регулювання характеристик контакту з органічного напівпровідника Рс структур Al/РсAl/por-Si/n-Si/ITO І Cu/РсСu/ por-Si/n-Sі/ITO/ Є.І.Зубко, Є. Я. Швець// Радіоелектроніка та автоматика.2015.№2. С.37– 45.

У результаті дослідження впливу легування на характер контактів з органічних напівпровідників Рс була створена технологія і апаратура управління процесами коригування легуючих домішок, за якою виявлено оборотне поглинання кисню зі зміною характера контакту від омічного до випрямляючого для Cu/РсСu/por-Si/n-Sі/ITO. Для структур Al/РсAl/por-Si/n-Si/ITO коригування характеристик РсAl здійснюють після операцій плазмового травлення в суміші газів Сl2 і N2 в плині 2 годин та відпалу зразка при 200°С при дії кисню.

Іл. 9. Бібліогр.: 7 назв.

UDC 621.383.52:537.311.4

Research of technology and equipment which controls processes of correcting alloying components for regulation of characteristics of contact made of organic semiconductor Pc of structures Al/PcAl/por-Si/n-Si/ITO and Cu/РсСu/por-Si/n-Sі/ITO/E.I.Zubko, Е.Y.Shvets// Radioelektronica i informatika. 2015. № 2 P. 37–45.

As a result of research is determined influence of doping on character of contacts from organic semiconductors Рс. The technology and equipment for control of correcting of alloying impurity allows detected turnaround absorption of oxygen with change of character of contact from ohmic to rectifying for Cu/РсСu/por-Si/n-Sі/ITO. For structures Al/РсAl/por-Si/n-Si/ITO a correcting of characteristics РсAl were performed after operations of plasma etching in a mix of gases Сl2 and N2 for 2 hours and annealing the sample at 200°С in atmosphere of oxygen.

Fig. 9. Ref.: 7 items.

Литература:

  1. Когаловский М.Р. Перспективные технологии информационных систем. М.: ДМК Пресс, 2003. 288 с.
  2. Спирли Э. Корпоративные хранилища данных. Планирование, разработка, развитие / Э. Спирли. М. : Издательский дом “Вильямс”, 2001. 400 с.
  3. Артемьева И.Л. Многоуровневые модели предметных областей и методы их разработки [Текст] // 10-я нац. конф. по ИИ, Обнинск, 25-28 сент. 2006: сб. тр. в 3-х томах. М.: Физматлит, 2006. Т. 1. С. 44 – 51.
  4. Арсеньев Б.П., Яковлев С.А. Интеграция распределенных баз данных. Спб.: Издательство «Лань», 2001. 464 с.
  5. Цаленко М.Ш. Типология и системный анализ информационных систем // Сборник трудов. М.: ВНИИСИ, 1992. Вып 1. С. 16 – 24.
  6. Green P., Using Meta Models for the Comparison of Ontologies / P. Green, I. Davies, S.K. Milton, M. Rosemann // Proc. of the Eighth CAiSE/IFIP8.1 International Workshop on the Evaluation of Modeling Methods in Systems Analysis and Design. Austria, June 2003. 12 p.
  7. Jarke M., Heterogeneity in Model Management: A Meta Modeling Approach / M. Jarke, M.A. Jeusfeld, HW. Nissen, C. Quix // Conceptual Modeling: Foundations and Applications, Essays in Honor of John Mylopoulos. Berlin: Springer-Verlag, 2009. P. 237-253.
  8. Гарсиа-Молина Г. Системы баз данных. Полный курс.: Пер. с англ. / Гарсиа-Молина Г., Ульман Дж., Уидом Дж. М.: Издательский дом „Вильямс“, 2003.
  9. Цикритзис Д., Лоховски Ф. Модели данных. М.: Финансы и статистика, 1985. 344 с.
  10. Мальцев А. И. Алгоритмы и рекурсивные функции. М.: Наука, 1965. 245 с.
  11. Танянский C.C. Семантическая модель предметной области в задачах интеграции неоднородных информационных систем // Вестник Херсонского национального технического университета. Херсон: ХНТУ, 2005. №1(21). С. 52-59.
  12. Пономаренко Л.А., Танянский С.С., Филатов В.А. Интеграция информационных систем при частичном отображении моделей данных // Проблемы системного подхода в экономике. 2008. Вып. 26. С. 33-44.

Transliterated bibliography:

  1. Kogalovskij M.R. Perspektivnye tehnologii informacionnyh sistem. M.: DMK Press, 2003. 288 s.
  2. Spirli Je. Korporativnye hranilishha dannyh. Planirovanie, razrabotka, razvitie / Je. Spirli. M. : Izdatel'skij dom “Vil'jams”, 2001. 400 s.
  3. Artem'eva I.L. Mnogourovnevye modeli predmetnyh oblastej i metody ih razrabotki [Tekst] // 10-ja nac. konf. po II, Obninsk, 25-28 sent. 2006: sb. tr. v 3-h tomah. M.: Fizmatlit, 2006. T. 1. S. 44 – 51.
  4. Arsen'ev B.P., Jakovlev S.A. Integracija raspredelennyh baz dannyh. Spb.: Izdatel'stvo «Lan'», 2001. 464 s.
  5. Calenko M.Sh. Tipologija i sistemnyj analiz informacionnyh sistem // Sbornik trudov. M.: VNIISI, 1992. Vyp 1. S. 16 – 24.
  6. Green P., Using Meta Models for the Comparison of Ontologies / P. Green, I. Davies, S.K. Milton, M. Rosemann // Proc. of the Eighth CAiSE/IFIP8.1 International Workshop on the Evaluation of Modeling Methods in Systems Analysis and Design. Austria, June 2003. 12 p.
  7. Jarke M., Heterogeneity in Model Management: A Meta Modeling Approach / M. Jarke, M.A. Jeusfeld, HW. Nissen, C. Quix // Conceptual Modeling: Foundations and Applications, Essays in Honor of John Mylopoulos. Berlin: Springer-Verlag, 2009. P. 237-253.
  8. Garsia-Molina G. Sistemy baz dannyh. Polnyj kurs.: Per. s angl. / Garsia-Molina G., Ul'man Dzh., Uidom Dzh. M.: Izdatel'skij dom „Vil'jams“, 2003.
  9. Cikritzis D., Lohovski F. Modeli dannyh. M.: Finansy i statistika, 1985. 344 s.
  10. Mal'cev A. I. Algoritmy i rekursivnye funkcii. M.: Nauka, 1965. 245 s.
  11. Tanjanskij C.C. Semanticheskaja model' predmetnoj oblasti v zadachah integracii neodnorodnyh informacionnyh sistem // Vestnik Hersonskogo nacional'nogo tehnicheskogo universiteta. Herson: HNTU, 2005. №1(21). S. 52-59.
  12. Ponomarenko L.A., Tanjanskij S.S., Filatov V.A. Integracija informacionnyh sistem pri chastichnom otobrazhenii modelej dannyh // Problemy sistemnogo podhoda v jekonomike. 2008. Vyp. 26. S. 33-44.

Божинский Иван Андреевич, канд. техн. наук, зам. начальника НИЧ ХНУРЭ. Научные интересы: информационные системы. Адрес: Украина, 61166, Харьков, пр. Ленина, 14, тел. 70-21-378.

 30-36
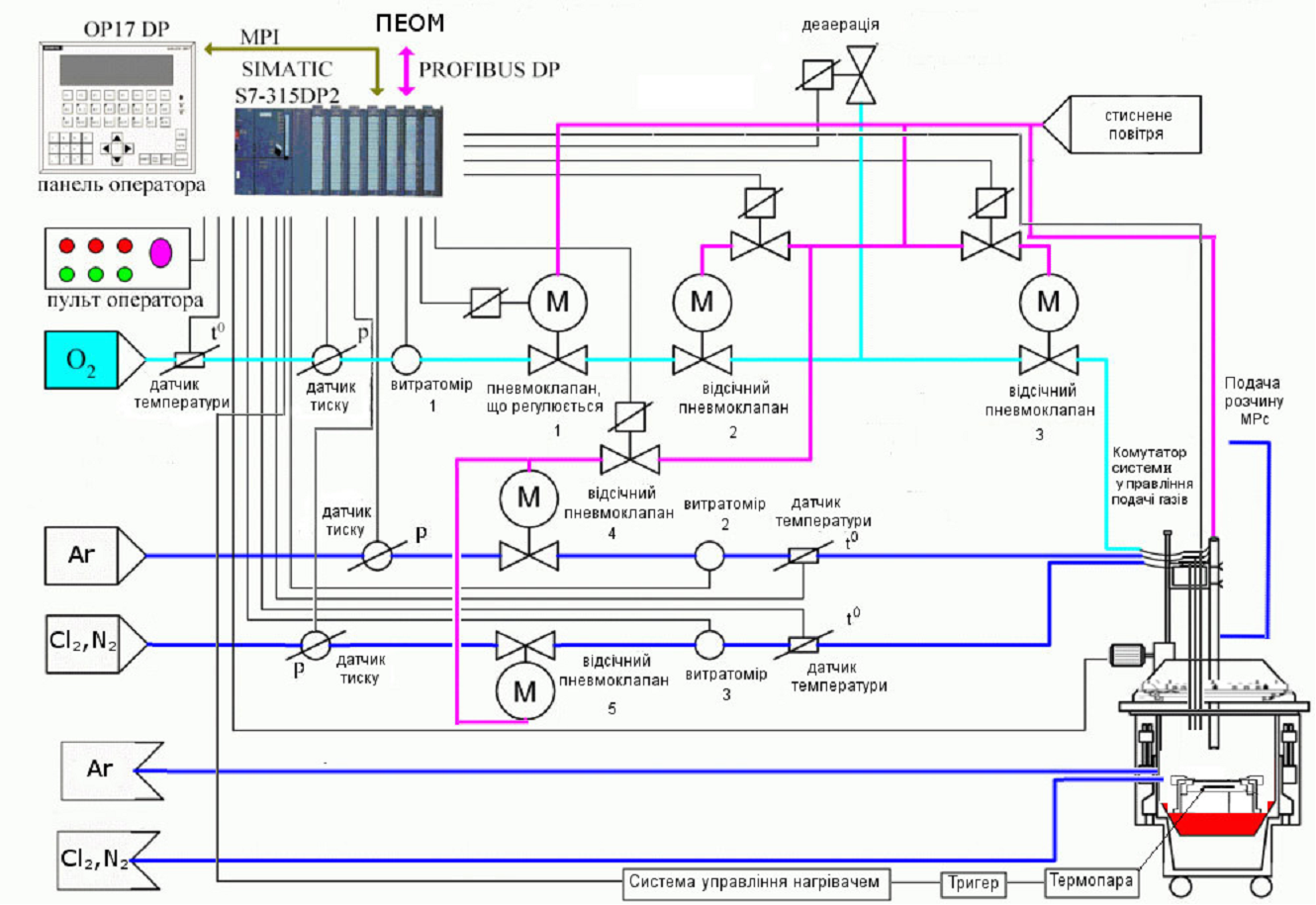ЗУБКО Є.І., ШВЕЦЬ Є.Я. РОЗРОБКА ТЕХНОЛОГІЇ І АПАРАТУРИ УПРАВЛІННЯ КОРИГУВАННЯМ ЛЕГУЮЧИХ ДОМІШОК ДЛЯ РЕГУЛЮВАННЯ ХАРАКТЕРИСТИК КОНТАКТУ З ОРГАНІЧНОГО НАПІВПРОВІДНИКА РС СТРУКТУР AL/РСAL/POR-SI/N-SI/ITO І CU/РССU/ POR-SI/N-SІ/ITO

Розробляється технологія і апаратура управління процесами коригування легуючих домішок з метою регулювання характеристик додаткового контакту з РсСu, РсAl структур Cu/РсСu/por-Si/n-Sі/ITO, Al/РсAl/por-Si/n-Si/ITO, за якою виявляється оборотне поглинання кисню зі зміною характеру контакту від омічного до випрямляючого для Cu/РсСu/por-Si/n-Sі/ITO. Для структур Al/РсAl/por-Si/n-Si/ITO коригування характеристик РсAl здійснюють після операцій плазмового травлення в суміші газів Сl2 і N2 в плині 2 годин, внаслідок утворення тонкого запорного шару Al2O3.

Ключові слова: кисень, повітря, фталоцианін міді, фталоцианін алюмінію, оборотне поглинання.

Кey words: oxygen, air, phtalocianin copper, phtalocianin aluminium, reversible absorption.

Література:

  1. Simon J., Andre J. J. Molecular semiconductors; Lehn J.M.; Rees C.W. Berlin: Springer-Verlag, 1985. 344 p.
  2. Юрре Т. А., Рудая Л. И., Климова  Н. В., Шаманин В. В. Органические материалы для фотовольтаических и светоизлучающих устройств // Физика и техника полупроводников. 2003. Т. 37, № 7. С. 835 - 843.
  3. ПахомовЛ.Г., Леонов Е. С. Пленочные структуры на основе органических полупроводников // Учебно-методические материалы по программе повышения квалификации «Физико-химические основы нанотехнологий». Нижний Новгород: Нижегородский государственный университет им. Н. И. Лобачевского, 2007. 79 с.
  4. Гутман Ф., Лайонс Л. Органические полупроводники. М.: Мир, 1970. 696 с.
  5. Зубко Є. І. Спосіб виготовлення контактого шару на антивідбиттєвому покритті сонячного елемента. Патент на корисну модель № 67830. Україна, Опубл. 12.03.2012. Бюл. № 5, С. 4.
  6. Wright J. D. Gas adsorption on phthalocyanines and its effects on electrical properties // Progr. Surf. Sci. 1989. № 31. Р. 1-60.
  7. ГалперинВ.А., Данилкин Е. В., Мочалов А. И. Процессы плазменного травления в микро- и нанотехнологиях // Учебное пособие. М.: Бином, Лаборатория знаний, 2013. 283 с.

Зубко Євгенія Іванівна, пров. спец. кафедри мікроелектронних інформаційних систем Запорізької державної інженерної академії. Наукові інтереси: технологія виготовлення, дослідження і моделювання низькорозмірних структур для потреб фотовольтаїки і сенсорики. Адреса: Україна, 69000, Запоріжжя, вул. Добролюбова, 22, тел.: (061) 2393987. Email: evgeniya-zubko@mail.ru

Швець Євген Якович, канд. техн. наук., професор, в. о. ректора Запорізької державної інженерної академії. Наукові інтереси: методи дослідження параметрів сонячних елементів. Адреса: Україна, 69000, Запоріжжя, вул. Добролюбова, 22, тел.: (061) 2393987. Email: evgeniya-zubko@mail.ru

 37-44
ПОДГОРНЫЙ А.Р., СИДОРОВ М.В., ЯЛОВЕГА И.Г. ЧИСЛЕННЫЙ АНАЛИЗ ФАЗОВЫХ ПРЕВРАЩЕНИЙ НА ПРИМЕРЕ ОДНОМЕРНОЙ ЗАДАЧИ СТЕФАНА

Рассматривается задача расчета температурного поля в стержне при наличии фазовых превращений (одномерная задача Стефана). На основании метода Галеркина для нестационарных задач строится численный метод решения задачи Стефана. Эффективность численного метода иллюстрируется серией вычислительных экспериментов.

Ключевые слова: одномерная задача Стефана, точка фазового перехода, метод Галеркина.

Key words: one-dimensional Stefan problem, of phase transitions point, the Galerkin method.

УДК 519.63

Чисельний аналіз фазових перетворень на прикладі одновимірної задачі Стефана / О.Р. Подгорний, М.В. Сидоров, І.Г. Яловега // Радіоелектроніка та інформатика. 2015. № 2. С. 45–48.

Розглянуто задачу розрахунку процесу теплопровідності на відрізку при наявності фазових перетворень (одновимірна задача Стефана). Для її чисельного аналізу запропоновано наближено-аналітичний метод, який базується на методі Гальоркіна. Проведено розрахунки для модельної задачі.

Іл. 1. Бібліогр.: 9 назв.

UDC 519.63

Numerical analysis of phase transformations on the example of one-dimensional Stefan problem / A.R. Podgornyj, M.V. Sidorov, I.G. Yalovega // Radioelektronica i informatika. 2015. № 2. P. 45–48.

The problem of calculating the process of thermal conductivity on the segment in the presence of phase transitions (one-dimensional Stefan problem) was considered. For its numerical analysis the approximate analytical method based on the Galerkin method was suggested. The calculations for the model problem were conducted.

Fig. 1. Ref.: 9 items.

Литература:

  1. Прусаков Г.М. Математические модели и методы в расчетах на ЭВМ. М.: Наука, 1993. 144 с.
  2. Левин В.И. Араманович И.Г. Уравнения математической физики. М.: Наука, 1969. 288 с.
  3. Подгорный А.Р. Численный анализ одной задачи фазовых превращений // Научные труды Международной молодёжной научной конференция «XL Гагаринские чтения» в 9 томах (Москва, «МАТИ» – РГТУ им. К.Э. Циолковского, 7 – 11 апреля 2014). Т. 5. С. 158 – 160.
  4. Подгорный А.Р. Об одной проблеме математического моделирования фазовых превращений // Материалы XVIII Международного молодежного форума «Радиоэлектроника и молодежь в XXI веке» (Харьков, ХНУРЭ, 14 – 16 апреля 2014). Т. 7. С. 130 – 131.
  5. Самарский А.А., Вабищевич П.Н. Вычислительная теплопередача. М.: Едиториал УРСС, 2003. 784 с.
  6. Мартинсон Л.К., Малов Ю.И. Дифференциальные уравнения математической физики. 2-е изд. М.: Изд-во МГТУ им. Н.Э. Баумана, 2002. 368 с.
  7. Михлин С.Г. Численная реализация вариационных методов. М.: Наука, 1966. 432 с.
  8. Подгорный А.Р. Математическое моделирования фазовых превращений на примере одномерной задачи Стефана // Материалы XIX Международного молодежного форума «Радиоэлектроника и молодежь в XXI веке» (Харьков, ХНУРЭ, 20 – 22 апреля 2015). Т. 7. С. 84 – 85.
  9. Подгорний О.Р. Математичне моделювання фазових перетворень на прикладі одновимірної задачі Стефана // Тези доповідей Вісімнадцятої Всеукраїнської (Тринадцятої Міжнародної) студентської наукової конференції з прикладної математики та інформатики „СНКПМI-2015” (Львів, ЛНУ ім. І.Франка, 22 – 23 квітня 2015). С. 133 – 135.

Транслитерированный список литературы.

  1. Prusakov G.M. Matematicheskie modeli i metody v raschetah na EVM. M.: Nauka, 1993. 144 p.
  2. Levin V.I. Aramanovich I.G. Uravnenija matematicheskoj fiziki. M.: Nauka, 1969. 288 p.
  3. Podgornyj A.R. Chislennyj analiz odnoj zadachi fazovyh prevrashhenij // Nauchnye trudy Mezhdunarodnoj molodjozhnoj nauchnoj konferencija «XL Gagarinskie chtenija» v 9 tomah (Moskva, «MATI» – RGTU im. K.E. Ciolkovskogo, 7 – 11 aprelja 2014). T. 5. Pp. 158 – 160.
  4. Podgornyj A.R. Ob odnoj probleme matematicheskogo modelirovanija fazovyh prevrashhenij // Materialy XVIII Mezhdunarodnogo molodezhnogo foruma «Radiojelektronika i molodezh' v XXI veke» (Har'kov, KhNURE, 14 – 16 aprelja 2014). T. 7. Pp. 130 – 131.
  5. Samarskij A.A., Vabishhevich P.N. Vychislitel'naja teploperedacha. M.: Editorial URSS, 2003. 784 p.
  6. Martinson L.K., Malov Ju.I. Differencial'nye uravnenija matematicheskoj fiziki. 2-e izd. M.: Izd-vo MGTU im. N.E. Baumana, 2002. 368 p.
  7. Mihlin S.G. Chislennaja realizacija variacionnyh metodov. M.: Nauka, 1966. 432 p.
  8. Podgornyj A.R. Matematicheskoe modelirovanija fazovyh prevrashhenij na primere odnomernoj zadachi Stefana // Materialy XIX Mezhdunarodnogo molodezhnogo foruma «Radiojelektronika i molodezh' v XXI veke» (Har'kov, KhNURE, 20 – 22 aprelja 2015). T. 7. Pp. 84 – 85.
  9. Podgornyj O.R. Matematychne modeljuvannja fazovyh peretvoren' na prykladi odnovymirnoi' zadachi Stefana // Tezy dopovidej Visimnadcjatoi' Vseukrai'ns'koi' (Trynadcjatoi' Mizhnarodnoi') students'koi' naukovoi' konferencii' z prykladnoi' matematyky ta informatyky „SNKPMI-2015” (L'viv, LNU im. I.Franka, 22 – 23 kvitnja 2015). Pp. 133 – 135.

Подгорний Алексей Русланович, магистрант кафедры прикладной математики ХНУРЭ. Научные интересы: математическое моделирование и вычислительная математика, программирование. Адрес: Украина, 61166, Харьков, пр. Ленина, 14, тел. (057) 7021436.

Сидоров Максим Викторович, канд. физ.-мат. наук, доц. каф. прикладной математики ХНУРЭ. Научные интересы: математическое моделирование, численные методы, математическая физика, теория R-функций и её приложения, стохастический анализ и его приложения. Адрес: Украина, 61166, Харьков, пр. Ленина, 14, тел. (057) 7021436.

Яловега Ирина Георгиевна, канд. техн. наук, доц. каф. математики ХНПУ им. Г.С. Сковороды. Научные интересы: математическое моделирование, методика преподавания математики. Адрес: Украина, 61168, Харьков, ул. Блюхера, 2.

Podgornyj Alexej Ruslanovich, undergraduate of Department of Applied Mathematics KhNURE. Research interests: mathematical modeling and computational mathematics, programming. Address: Ukraine, 61166, Kharkov, Lenin Ave, 14, phone +38 (057) 7021436.

Sidorov Maxim Victorovich, Ph.D. in Physics and Maths, associate professor, associate professor of Department of Applied Mathematics KhNURE. Research interests: mathematical modeling, numerical methods, mathematical physics, R-functions theory and its applications, stochastic analysis and its applications. Address: Ukraine, 61166, Kharkov, Lenin Ave, 14, phone +38 (057) 7021436.

Yalovega Irina Georgievna, Ph.D. in Engineering, associate professor of Department of Mathematics H.S. Skovoroda KhNPU. Research interests: mathematical modeling, methods of teaching mathematics. Address: Ukraine, 61168, Kharkov, Bluher St., 2.

 45-48
ЛАМТЮГОВА С.Н. ПРИМЕНЕНИЕ ИТЕРАЦИОННЫХ МЕТОДОВ К РАСЧЕТУ ОБТЕКАНИЯ ТЕЛ СТАЦИОНАРНЫМ ПОТОКОМ ВЯЗКОЙ ЖИДКОСТИ

Рассматривается и обосновывается применение методов R-функций, последовательных приближений и Бубнова-Галёркина к расчету стационарного обтекания тел вращения и цилиндрических тел вязкой несжимаемой жидкостью.

Ключевые слова: вязкая жидкость, функция тока, метод R-функций, метод последовательных приближений, метод Бубнова-Галёркина.

Key words: viscous fluid, stream function, the R-functions method, the method of successive approximations, the Bubnov-Galerkin method.

УДК 517.9:532.5

Застосування ітераційних методів до розрахунку обтікання тіл стаціонарним потоком в’язкої рідини / С.М. Ламтюгова // Радіоелектроніка та інформатика. 2015. № 2. С. 49 – 56.

Розглянуто і обґрунтовано застосування методів R-функцій, послідовних наближень і Бубнова-Гальоркіна до розрахунку обтікання тіл обертання і циліндричних тіл стаціонарним потоком в’язкої рідини. Доведено збіжність побудованого ітераційного процесу при малих числах Рейнольдса, отримані оцінки швидкості збіжності і оцінки розв’язків у енергетичній нормі.

Бібліогр.: 23 назв.

UDC 517.9:532.5

The iterative methods application for calculating the flow over body by stationary current of viscous fluid / S.N. Lamtyugova // Radioelektronica i informatika. 2015. № 2. P. 49–56.

The application of the R-functions method, the successive approximations method and the Bubnov-Galerkin method to calculate the flow over bodies of revolution and around cylindrical bodies by stationary current of viscous fluid was considered and substantiated. The convergence of the iterative process, constructed at low Reynolds numbers, was proved. The estimates of the convergence rate and solutions assessments in the energy norm were derived.

Ref.: 23 items.

Литература:

  1. Ламб Г. Гидродинамика. М.: РХД, 2003. Т. 1. 452 с.; Т. 2. 452 с.
  2. Ландау Л.Ф., Лифшиц Е.М. Теоретическая физика. В 10 т. Т. VI. Гидродинамика. М.: Физматлит, 2003. 736 с.
  3. Лойцянский Л.Г. Механика жидкости и газа. М.: Дрофа, 2003. 840 с.
  4. Кутепов А.М., Полянин А.Д., Запрянов З.Д., Вязьмин А.В., Казенин Д.А. Химическая гидродинамика. М.: Квантум, 1996. 336 с.
  5. Хаппель Дж., Бреннер Г. Гидродинамика при малых числах Рейнольдса. М.: Мир, 1976. 630 с.
  6. Шкадов В.Я., Запрянов З.Д. Течения вязкой жидкости. М.: Изд-во Моск. ун-та, 1984. 200 с.
  7. ПолянинА.Д., Зайцев В.Ф. Справочник по нелинейным уравнениям математической физики: Точные решения. М.: Физматлит, 2002. 432 с.
  8. Рвачев В.Л. Теория R-функций и некоторые ее приложения. К.: Наук. думка, 1982. 552 с.
  9. Колосова С.В. Применение проекционных методов и метода R-функций к решению краевых задач в бесконечных областях. Дисс. … к.ф.-м.н.: 01.01.07 Вычислительная математика. Харьков: ХИРЭ, 1972. 85 с.
  10. Колосова С.В., Сидоров М.В. Применение метода R–функций к расчету плоских течений вязкой жидкости // Вісн. ХНУ. Сер. Прикл. матем. і мех. 2003. № 602. С. 61–67.
  11. Суворова И.Г. Компьютерное моделирование осесимметричных течений жидкости в каналах сложной формы // Вестн. НТУ ХПИ. Харьков, 2004. № 31. С. 141–148.
  12. Тевяшев А.Д., Гибкина Н.В., СидоровМ.В. Об одном подходе к математическому моделированию плоских стационарных течений вязкой несжимаемой жидкости в конечных односвязных областях // Радиоэлектроника и информатика. 2007. № 2. С. 50–57.
  13. Максименко-Шейко К.В. Математическое моделирование теплообмена при движении жидкости по каналам с винтовым типом симметрии методом R-функций // Доп. НАН України. 2005. № 9. С. 41–46.
  14. Стрельченко А.Й., Колосова С.В., РвачовВ.Л. Про один метод розв’язування крайових задач // Доп. АН УРСР, сер. А. № 9. 1972. С. 837–839.
  15. Киселев А.А., Ладыженская О.А. О решении линеаризованных уравнений плоского нестационарного течения вязкой несжимаемой жидкости // ДАН СССР. 1954. Т. XCV, № 6. С. 1161–1164.
  16. Ладыженская О.А. Математические вопросы динамики вязкой несжимаемой жидкости. М.: Наука, 1970. 288 с.
  17. Михлин С.Г. Вариационные методы в математической физике. М.: Наука, 1970. 512 с.
  18. Михлин С.Г. Некоторые достаточные условия сходимости метода Галеркина // Уч. зап. ЛГУ. Сер. мат. н. 1950. Вып. 21, № 135. С. 3–23.
  19. Полянин А.Д. Справочник по линейным уравнениям математической физики. М.: Физматлит, 2001. 576 с.
  20. Ламтюгова С.Н., Сидоров М.В. Математическое моделирование задач обтекания в цилиндрической системе координат // Вісник ХНУ ім. В.Н. Каразіна. Сер. Математичне моделювання. Інформаційні технології. Автоматизовані системи управління. 2014. №1105, вип. 24. С. 111–121.
  21. Lamtyugova S.N., Sidorov M.V. Numerical analysis of the problem of flow past a cylindrical body applying the R-functions method and the Galerkin method // Econtechmod. 2014. Vol. 3, No. 3. P. 43‑50.
  22. Chueshov I., Duan J., Schmalfuss B. Probabilistic dynamics of two-layer geophysical flows // Stochastics and dynamics. 2001. Vol. 1, No. 4. P. 451–475.
  23. Lamtyugova S.N., Sidorov M.V. Numerical analysis of the external slow flows of a viscous fluid using the R-function method // Journal of Engineering Mathematics, 2015. V. 91, No. 1. P. 59–79. (DOI: 10.1007/s10665-014-9746-x).

Транслитерированный список литературы.

  1. Lamb G. Gidrodinamika. M.: RHD, 2003. T. 1. 452 p.; T. 2. 452 p.
  2. Landau L.F., Lifshic E.M. Teoreticheskaja fizika. V 10 t. T. VI. Gidrodinamika. M.: Fizmatlit, 2003. 736 p.
  3. Lojcjanskij L.G. Mehanika zhidkosti i gaza. M.: Drofa, 2003. 840 p.
  4. Kutepov A.M., Poljanin A.D., Zaprjanov Z.D., Vjaz'min A.V., Kazenin D.A. Himicheskaja gidrodinamika. M.: Kvantum, 1996. 336 p.
  5. Happel' Dzh., Brenner G. Gidrodinamika pri malyh chislah Rejnol'dsa. M.: Mir, 1976. 630 p.
  6. Shkadov V.Ja., Zaprjanov Z.D. Techenija vjazkoj zhidkosti. M.: Izd-vo Mosk. un-ta, 1984. 200 p.
  7. Poljanin A.D., Zajcev V.F. Spravochnik po nelinejnym uravnenijam matematicheskoj fiziki: Tochnye reshenija. M.: Fizmatlit, 2002. 432 p.
  8. Rvachev V.L. Teorija R-funkcij i nekotorye ee prilozhenija. K.: Nauk. dumka, 1982. 552 p.
  9. Kolosova S.V. Primenenie proekcionnyh metodov i metoda R-funkcij k resheniju kraevyh zadach v besko-nechnyh oblastjah. Diss. … k.f.-m.n.: 01.01.07 Vychislitel'naja matematika. Har'kov: HIRJe, 1972. 85 p.
  10. Kolosova S.V., Sidorov M.V. Primenenie metoda R–funkcij k raschetu ploskih techenij vjazkoj zhidkosti // Vіsn. HNU. Ser. Prikl. matem. і meh. 2003. № 602. Pp. 61–67.
  11. Suvorova I.G. Komp'juternoe modelirovanie osesimmetrichnyh techenij zhidkosti v kanalah slozhnoj formy // Vestn. NTU HPI. Har'kov, 2004. № 31. Pp. 141–148.
  12. Tevjashev A.D., Gibkina N.V., Sidorov M.V. Ob odnom podhode k matematicheskomu modelirovaniju ploskih stacionarnyh techenij vjazkoj neszhimaemoj zhidkosti v ko-nechnyh odnosvjaznyh oblastjah // Radiojelektronika i in-formatika. 2007. № 2. Pp. 50–57.
  13. Maksimenko-Shejko K.V. Matematicheskoe modelirovanie teploobmena pri dvizhenii zhidkosti po kanalam s vintovym tipom simmetrii metodom R‑funkcij // Dop. NAN Ukraїni. 2005. № 9. Pp. 41–46.
  14. Strel'chenko A.J., Kolosova S.V., Rvachov V.L. Pro odin metod rozv’jazuvannja krajovih zadach // Dop. AN URSR, ser. A. № 9. 1972. Pp. 837–839.
  15. Kiselev A.A., Ladyzhenskaja O.A. O reshenii linearizovannyh uravnenij ploskogo nestacionarnogo techenija vjazkoj neszhimaemoj zhidkosti // DAN SSSR. 1954. T. XCV, № 6. Pp. 1161–1164.
  16. Ladyzhenskaja O.A. Matematicheskie voprosy dinamiki vjazkoj neszhimaemoj zhidkosti. M.: Nauka, 1970. 288 p.
  17. Mihlin S.G. Variacionnye metody v matematicheskoj fizike. M.: Nauka, 1970. 512 p.
  18. Mihlin S.G. Nekotorye dostatochnye uslovija shodimosti metoda Galerkina // Uch. zap. LGU. Ser. mat. n. 1950. Vyp. 21, № 135. Pp. 3–23.
  19. Poljanin A.D. Spravochnik po linejnym uravnenijam matematicheskoj fiziki. M.: Fizmatlit, 2001. 576 з.
  20. Lamtjugova S.N., Sidorov M.V. Matematicheskoe modelirovanie zadach obtekanija v cilindricheskoj sisteme koordinat // Vіsnik HNU іm. V.N. Karazіna. Ser. Matematichne modeljuvannja. Іnformacіjnі tehnologії. Avtomatizovanі sistemi upravlіnnja. 2014. №1105, vip. 24. Pp. 111–121.
  21. Lamtyugova S.N., Sidorov M.V. Numerical analysis of the problem of flow past a cylindrical body applying the R-functions method and the Galerkin method // Econtechmod. 2014. Vol. 3, No. 3. Pp. 43‑50.
  22. Chueshov I., Duan J., Schmalfuss B. Probabilistic dynamics of two-layer geophysical flows // Stochastics and dynamics. 2001. Vol. 1, No. 4. Pp. 451–475.
  23. Lamtyugova S.N., Sidorov M.V. Numerical analysis of the external slow flows of a viscous fluid using the R-function method // Journal of Engineering Mathematics, 2015. V. 91, No. 1. Pp. 59–79. (DOI: 10.1007/s10665-014-9746-x).

Ламтюгова Светлана Николаевна, аспирантка каф. прикладной математики ХНУРЭ, ассистент каф. высшей математики ХНУГХ им. А.Н. Бекетова. Научные интересы: математическое моделирование, численные методы, математическая физика, теория R-функций и её приложения. Адрес: Украина, 61166, Харьков, пр. Ленина, 14, тел. +38 (057) 7021436.

Lamtyugova Svetlana Nikolaevna, PhD student of Department of Applied Mathematics KhNURE, Assistant of Department of Advanced Mathematics O.M. Beketov NUUE in Kharkiv. Research interests: mathematical modeling, numerical methods, mathematical physics, the theory of R-functions and its applications. Address: Ukraine, 61166, Kharkov, Lenin Ave, 14, phone +38 (057) 7021436.

 49-56
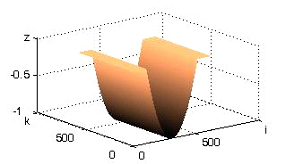ГРАБОВСЬКА Н.Р., РУСИН Б.П., ІВАНЮК В.Г., КАПШІЙ О.В. ПОХИБКА ТРИВИМІРНОЇ РЕКОНСТРУКЦІЇ ПОВЕРХНІ ТРІЩИНИ ЗА ТРІАДОЮ ЗОБРАЖЕНЬ

Розглядається метод тривимірної реконструкції поверхні за тріадою двомірних зображень, які отримані під різними напрямками освітлення. Оцінка похибки реконструкції похідних поверхні  проводиться  для двох бокових напрямків освітлення. Результати розрахунку демонструються на прикладі тестового зображення тріщини.

УДК 383.8:621.396.96:621.396.6

Похибка тривимірної реконструкції поверхні тріщини за тріадою зображень / Н.Р. Грабовська, Б.П. Русин, В.Г. Іванюк, О.В.Капшій // Радіоелектроніка і інформатика. 2015. № 2. С.57-62.

Розглянуто проблему оцінки похибки тривимірної реконструкції поверхні за двомірними зображеннями. Для відеозйомки зображень запропоновано використовувати три напрямки освітлення. Від точності встановлення напрямків освітлення визначально  залежить точність реконструкції. Проведено оцінку похибки реконструкції похідних поверхні залежно від  двох напрямків освітлення. Зокрема, на основі тестового зображення тріщини проведено розрахунок оцінки похибки реконструкції  похідних поверхні тріщини. В результаті аналізу отриманої  залежності представлені рекомендації  по встановленню експлуатаційних меж кутових відхилень напрямків освітлення та формуванню діапазонів реконструкції похідних.

Іл. 3. Бібліогр.: 16 назв.

UDC 383.8:621.396.96:621.396.6

An error of three-dimensional reconstruction of surface of crack is after the triad of images / Hrabovcska N.R., Rusyn B.P., Ivanyuk V.G., Kapshiy O.V. // Radioelektronika і informatika. 2015. № 2. P. 57-62.

The article considers the problem of error estimation for three-dimensional surface reconstruction with two-dimensional images. For recording  images it offers to use three directions of illumination. The accuracy of the determination of directions of illumination initially depends on the accuracy of the reconstruction. The estimation error of the reconstruction of the derivatives of the surface depending on two directions of illumination. In particular, based on the test image of the crack was calculated estimate of the error of reconstruction of the derivatives of the surface cracks. The analysis of this dependences presented recommendations for establishing operating limits of the angular deviations of the directions of illumination and formation ranges of the reconstruction of derivatives .

Fig.3. Ref.: 16 items.

Література:

  1. Sharland S. M. A review of the theoretical modeling of crevice and pitting corrosion Corrosion Science 1987. V. 27. N 3. P. 289-323.
  2. Marcus P. Corrosion mechanisms in theory and practice 2nd Edition - 2002. New York, Technology & Engineering – 742P.
  3. Y. Liu, X. Su, and Q. Zhang, “A novel encoded-phase technique for phase measuring profilometry,” Opt. Express 19(15), 2011. P.14137–14144 .
  4. Q. Zhang, X. Su, L. Xiang, and X. Sun, 3-D shape measurement based on complementary gray-code light, Opt. Lasers Eng., vol. 50, 2012. Р .574-579.
  5. S. Zhang, D. Van Der Weide, and J. Oliver, Superfast phase-shifting method for 3-D shape measurement, Opt. Express vol. 18, No. 9, 2010. P. 9684–9689.
  6. Woodham R.J. Photometric method for determining surface orientation from multiple images Optical Engineering. 1980. 19(1). Р.139–144.
  7. Maria E. Angelopoulou, Maria Petrou Evaluating the effect of diffuse light on photometric stereo reconstruction Machine Vision and Applications. 2014. Vol. 25, Issue 1. Р.199-210
  8. Yoshizawa, T. Handbook of Optical Metrology -principle and applications- CRC Press, New York 2009. 744 P.
  9. S. Zhang, High-resolution 3-D profilometry with binary phase-shifting methods, Appl. Opt.50(12). 2011. P.1753–1757.
  10. Sudipta N. Sinha, D. Scharstein, R. Szeliski. Efficient high-resolution stereo matching using local plane sweeps /. IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2014). 2014. P. 1219-1222.
  11. Richard Szeliski. Computer Vision: Algorithms and Applications. Springer, New York. 2010. 655 P.
  12. Неруйнівний контроль стану поверхонь, уражених корозійними пітингами /Б.П. Русин, Н.П. Ануфрієва, Н.Р. Грабовська, В.Г. Іванюк // Фіз.-хім. механіка матеріалів. 2013. №4. С. 90–96.
  13. Оцінка глибини тріщини за тріадою зображень / Б.П. Русин, В.Г. Іванюк, О.В. Капшій, Н.П. Ануфрієва // Радіоелектроніка і інформатика. 2010. №2. С. 70–78.
  14. Lambert. Photometria, sive de Mensura et gradibus luminis, colorum et umbrae / sumptibus viduae E. Klett, 1760.
  15. Shintaro Watanabe, Koji Miyajima Detecting Building Changes Using Epipolar Constraint From Aerial Images Taken At Different Positions // ICIP 2001. 2001. P.201-204.
  16. Смирнов В.И. Курс высшей математики. т. 1. М.: Наука. 1967.  480с.
  17. http://microtech-ua.com/

Transliterated bibliography:

  1. Sharland S. M. A review of the theoretical modeling of crevice and pitting corrosion Corrosion Science 1987. V. 27. N 3. – P. 289-323.
  2. Marcus P. Corrosion mechanisms in theory and practice 2nd Edition - 2002 – New York, Technology & Engineering – 742P.
  3. 3. Liu, X. Su, and Q. Zhang, “A novel encoded-phase technique for phase measuring profilometry,” Opt. Express 19(15), 2011. – P.14137–14144 .
  4. Q. Zhang, X. Su, L. Xiang, and X. Sun, 3-D shape measurement based on complementary gray-code light, Opt. Lasers Eng., vol. 50, 2012, p.574-579.
  5. S. Zhang, D. Van Der Weide, and J. Oliver, Superfast phase-shifting method for 3-D shape measurement, Opt. Express vol. 18, No. 9, 2010. P. 9684–9689.
  6. 6. Woodham R.J. Photometric method for determining surface orientation from multiple images Optical Engineering. 1980. – 19(1). – Р.139–144.
  7. 7. Maria E. Angelopoulou, Maria Petrou Evaluating the effect of diffuse light on photometric stereo reconstruction  Machine Vision and Applications. 2014, Vol. 25, Issue 1. – Р.199-210
  8. Yoshizawa, T. Handbook of Optical Metrology -principle and applications- CRC Press, New York 2009.- 744 P.
  9. S. Zhang, High-resolution 3-D profilometry with binary phase-shifting methods, Appl. Opt.50(12), 2011 P.1753–1757.
  10. Sudipta N. Sinha, D. Scharstein, R. Szeliski. Efficient high-resolution stereo matching using local plane sweeps. /. IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2014), 2014. P. 1219-1222.

11.http://www.opticsinfobase.org/oe/abstract.cfm?uri=oe-20-22-24139 - # Richard Szeliski. Computer Vision: Algorithms and Applications. Springer, New York, 2010.  655P.

  1. Nerujnivnyj kontrol' stanu poverhon', urazhenyh korozijnymy pityngamy /B.P. Rusyn, N.P. Anufrijeva, N.R. Grabovs'ka, V.G. Ivanjuk // Fiz.-him. mehanika materialiv. – 2013 –№4 –S. 90–96.
  2. Ocinka glybyny trishhyny za triadoju zobrazhen'. / B.P. Rusyn, V.G. Ivanjuk, O.V. Kapshij, N.P. Anufrijeva // Radioelektronika i informatyka. – 2010. – №2–S. 70–78.
  3. 14. J. H. Lambert,. Photometria, sive de Mensura et gradibus luminis, colorum et umbrae / sumptibus viduae E. Klett, 1760.
  4. Shintaro Watanabe, Koji Miyajima Detecting Building Changes Using Epipolar Constraint From Aerial Images Taken At Different Positions // ICIP 2001. – 2001. - P.201-204.
  5. Smyrnov V.Y. Kurs vjysshej matematyky. t. 1. – M.: Nauka. - 1967. - 480s.
  6. http://microtech-ua.com/

Грабовська Наталія Романівна, аспірантка Фізико-механічного інституту ім. Г.В.Карпенка НАНУ. Наукові інтереси: обробка та розпізнавання зображень. Адреса: Україна, 79601, Львів, вул. Наукова, 5а. dep32@ipm.lviv.ua

Русин Богдан Павлович, д-р техн. наук, проф., зав. відділом “Методів і систем дистанційного зондування “ Фізико-механічного інституту ім. Г.В.Карпенка НАНУ. Наукові інтереси: обробка та розпізнавання зображень. Адреса: Україна, 79601, Львів, вул. Наукова, 5а, e-mail: dep32@ipm.lviv.ua

Іванюк Віталій Григорович, інженер відділу “Методів і систем дистанційного зондування “ Фізико-механічного інституту ім. Г.В.Карпенка НАНУ. Наукові інтереси: обробка та розпізнавання зображень. Адреса: Україна, 79601,  Львів, вул. Наукова, 5а, тел:2296-530, e-mail: vivan@imp.lviv.ua

Капшій Олег Вірославович, канд. техн. наук, н.с відділу “Методів і систем дистанційного зондування “ Фізико-механічного інституту ім. Г.В.Карпенка НАНУ. Адреса: Україна, 79601,  Львів, вул. Наукова, 5а. тел: 22-96-530, e-mail: dep32@ipm.lviv.ua

Rusyn B.P., doctor of engineering sciences, professor, manager of department of "Methods and systems of the remote sensing " of Karpenko Physico- Mechanical Institute of NAS of Ukraine,  Address: 79601, Ukraine, Lviv, street Scientific, 5а, telephone : 2296-530, e - mail: dep32@ipm.lviv.ua

Hrabovcska N.R., graduate student of Karpenko Physico- Mechanical Institute of NAS of Ukraine,   Scientific interests: treatment and artificial perception. Address: 79601, Ukraine, Lviv, street Scientific, 5а, telephone: 2296-530, e - mail: dep32@ipm.lviv.ua

Ivanyuk V.G., engineer of department of "Methods and systems of the remote sensing " of Karpenko Physico- Mechanical Institute of NAS of Ukraine,  . Scientific interests: treatment and artificial perception. Address: 79601, Ukraine, Lviv, street Scientific, 5а, telephone: 2296-530, e - mail: vivan@imp.lviv.ua

Kapshiy O.V., a candidate of engineering sciences,  a research worker of department of "Methods and systems of the remote sensing " of Karpenko Physico- Mechanical Institute of NAS of Ukraine. Address: 79601, Ukraine, Lviv, street Scientific 5а., telephone: 22-96-530, e-mail: dep32@ipm.lviv.ua

 57-62